There's often talk of how nice it would be to have builtin tesselation support, which I fully agree with but at the same time I think an even more powerful alternative exists: Proper parallax that can truly create the illusion of displacement. While the default StandardMaterial3D shader has a Height section where a heightmap is used to indicate depth, the effect remains unrealistic even when using the Deep Parallax setting (Parallax Occlusion Mapping). The issue isn't even how bad the distortion can look sometimes, but rather how the effect is limited by the geometry of the surface it's on: If this hard limitation could be lifted efficiently we may achieve an incredible level of detail that trumps tesselation by using a ridiculously low number of polygons on the underlying mesh!


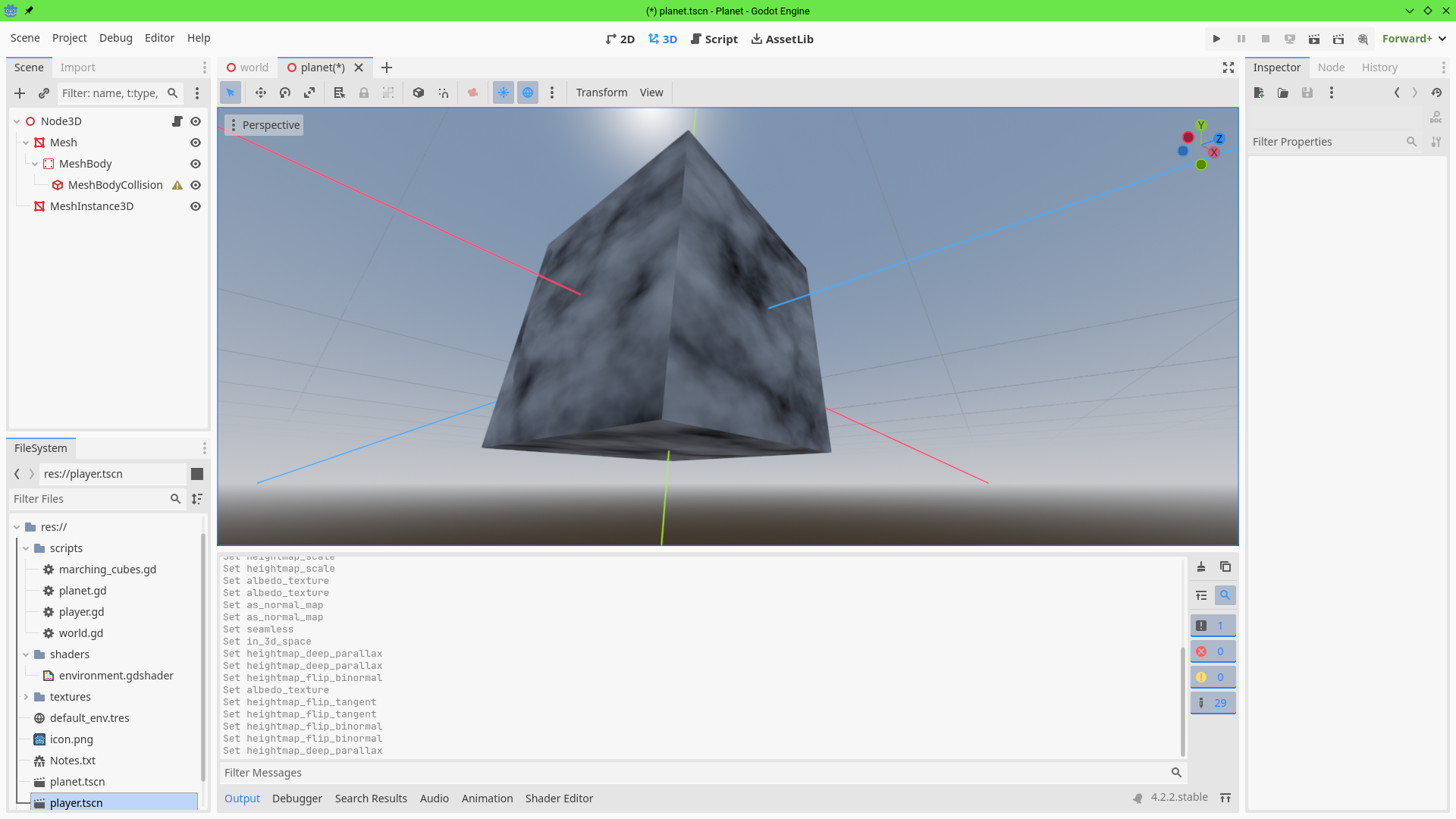
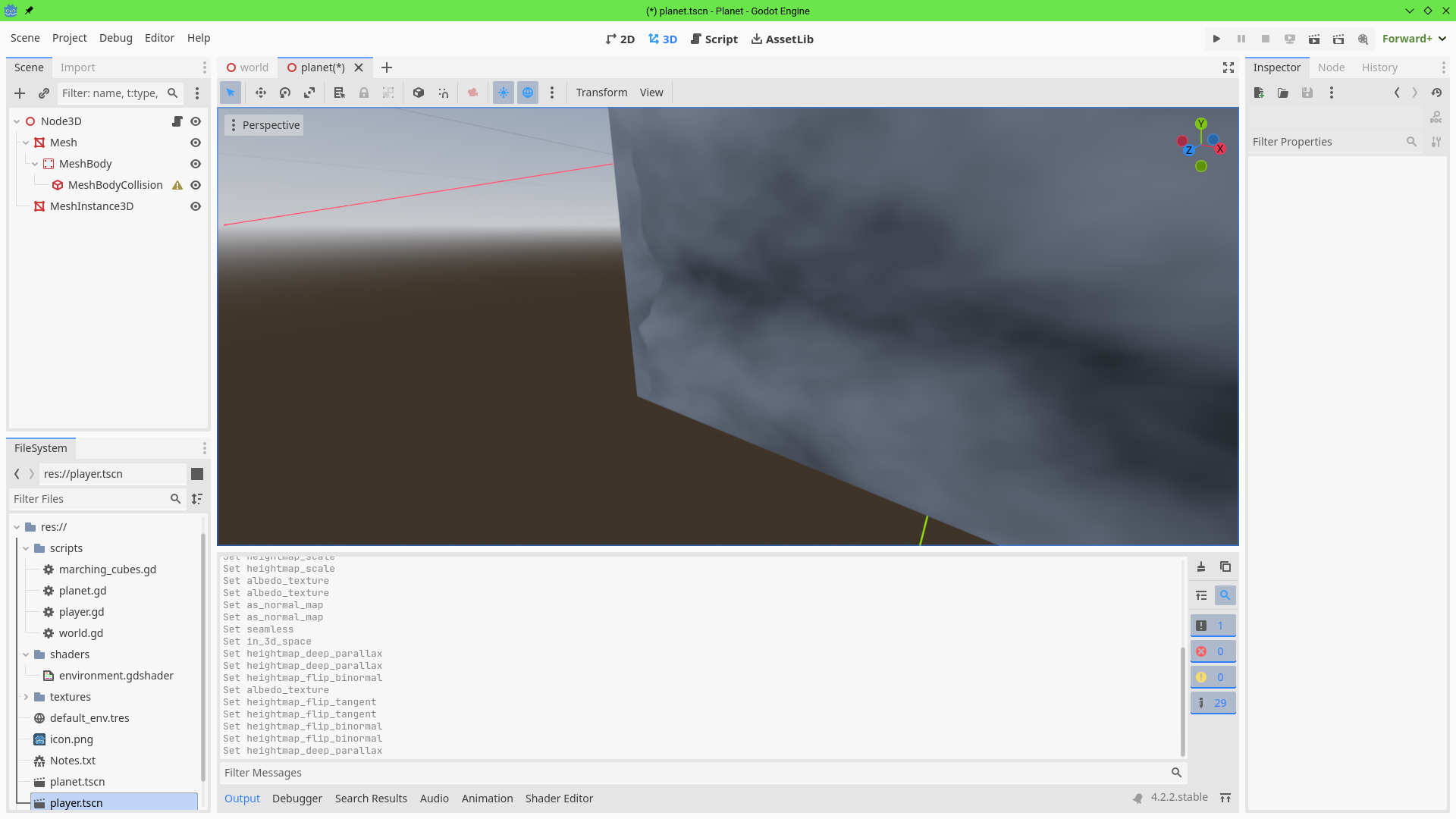
As can be seen in the images, the problem by far is that parallax can't pop out of the surface it's on: If you look at the edge of the cube you can still see a straight line... which isn't even limited to just those edges where the skybox is behind the cube, even interior edges connecting two faces from the camera's perspective can reveal the artificial line. We want high pixels to actually be rendered above the geometry surface and / or low pixels are to be rendered below it.

The problem is I'm not sure if either OpenGL or Vulkan shaders allow any way to do this: We're asking a pixel that doesn't initially overlap a triangle to behave as if it touched that triangle, shaders rely on a pixel touching their geometry for that shader to even be computed. At first this seems solvable by growing or shrinking the geometry in vertex shaders, if the faces are expanded to encompass the highest point on the parallax map lower points are then enclosed within the surface. But then what do you do when you detect a hole below an edge through which a pixel should proceed? The logical answer seems like using the alpha channel to mark that pixel as transparent so it can see through the surface... but is alpha is calculated before shaders and likely can't be edited retroactively: Every triangle would need to be rendered to a different pass so if we discard a pixel it may proceed to check a surface with a lower Z index than itself, which would likely butcher the renderer and GPU. The only solution seems like a mixture of material shader with post-process shader, where we check all triangles the pixel could touch apply the shrinkage / inflation of every pixel in its heightmap and if there's a hit artificially deviate the pixel to act like it's at a different position on the screen relative to that triangle.

I'm curious if any solution to this conundrum exists: Can shaders allow the parallax effect to pop out of the geometry the shader is on? So far not even a parallax shader for UE5 suggests this could be possible, they managed to achieve a very impressive effect but it's still bound to the geometry and you see a perfectly round sphere if you look at the edges. If there was some magic to get this solved, we could attain effects that surpass tesselation for far less resources... just add a few other needed effects like self-shadowing which someone seems to have already done for Godot 3 already!

  • xyz replied to this.

    MirceaKitsune Parallax mapping is still plain old texture mapping, although it can fool you it's magic. If you need "physically" displaced geometry, then well - displace it. Displacing individual pixels is not possible in modern gpu pipelines, that notion is simply incompatible with the whole concept of hardware accelerated rasterization. You can somewhat emulate it using volumetric rendering via ray marching, but that's quite performance costly and has other limitations.

      Megalomaniak The concept is pretty simple

      Not that simple 🙂. It still requires mesh pre-processing to displace the additional volume, as well as ray marching through it.

          xyz That's normally the rule: My hope was there might be some way to bend it. Surprised no one's yet tried to find a way to make a heightmap image pop out of a surface without having to use additional geometry; Real geometry is obviously ideal, but requires a lot of vertices which is far more costly and still won't look as good unless tessellated to pixel density.

          • xyz replied to this.

              MirceaKitsune Well the approach @Megalomaniak posted does this to an extent but it still needs a bit of additional geometry. It's simply not possible to make image pop out if there's no geometry because GPUs can only rasterize geometry and images are just mapped onto it. They can't displace pixels in 3d space in the way you seem to be expecting. It's just not how the hardware works.

                  xyz maybe some custom software renderer might be able to do it. A kind of a voxelization of the texels or something like a point cloud? But I don't really see the point(no pun intended). It would be more work for what wouldn't be much if at all a better result. Plus having to reinvent the wheel for everything like bone/armature skinning and animation. etc. Then again, there are efforts such as UE's nanite or that point cloud thingy for the UnLiMiTeD dEtAiL from some years back...

                      Megalomaniak Yeah, that's the thing: It's not something that would be mathematically impossible, just that it would take a lot of wizardry with the way shaders are currently designed. Such capabilities are things I wish folks thought about back when GPU designs and OpenGL were in early stages, it's a bit late now or at least must harder to do.

                      I remember how more than 10 years ago I was thinking we should have had tesselation without extra vertices at GPU level. It would be done, by interpreting the edges / surfaces between vertices as curves instead of straight lines interpolated based on where the pixel hits: You could get infinitely round surfaces without storing extra data via interpolation! Another thing we sadly never got... if we did we'd be used to low-poly models looking unusually round instead of pointy 😄

                          MirceaKitsune Oh, they did. Point clouds and voxels are actually nothing new. It's just that polygons are easier to rasterize and especially transform(to for example skeletally animate). So the industries choices have very much made sense TBH.

                          And I disagree that they are somehow harder to do now. Rather on the contrary, easier than ever before. Which is why we now have things like Nanite in UE. Or why ZBrush developer wrote the "2.5D" software renderer for the high poly sculpting taking advantage of tech like SSE when they did. Also note that ZBrush and Nanite still were designed to use polygons at the end of the day. For perfectly practical reasons.

                            MirceaKitsune It would be done, by interpreting the edges / surfaces between vertices as curves

                            What kind of curves?

                            I suggest implementing a simple software rasterizer to learn how the stuff works. You can then try to prototype your ideas on top of it to see if they actually make sense.

                                Megalomaniak Then again, there are efforts such as UE's nanite or that point cloud thingy for the UnLiMiTeD dEtAiL from some years back...

                                I never understood this obsession with infinite detail. The key to aesthetically pleasing imagery is in design and proportions, not in insurmountable heaps of detail. This is true for any pictorial medium, from classical painting to video games.

                                The apparent pixel displacement can be done by using voxels, but if we think about it, voxels are again just finer grained geometry.

                                  xyz The way 3D works in reality is vertices are connected by edges which form straight lines between which a triangle surface is drawn. What I imagined is if instead of a straight line, the edges and surface would act as curves, interpolated between the vertices based on the pixel's location. Essentially hardware subdivision surface or the way curves work in Godot and Blender, except without creating any extra vertices even temporarily. With such a system you'd pass a cube to the GPU and it would automatically draw a sphere from its 8 vertices.

                                  Technically it should be possible, but I imagine there's likely a good reason why this never caught on. Infinite detail always fascinated me and it's a dream any developer would probably like to achieve... especially the idea of doing it through interpolation so you don't have to store extra data, though computing it in realtime can be equally costly and negate the benefit.

                                      MirceaKitsune The way 3D works in reality is vertices are connected by edges which form straight lines between which a triangle surface is drawn.

                                      And how, pray tell do you imagine the process of rasterization for the curve without trigonometry? That was the question posed.

                                          MirceaKitsune Your complaint is equal to complaining why do we need to have pixels. It's because of digitalization, i.e. because we're doing the thing using a digital computer. A triangle is the simplest and most efficient way to represent a local "quant" of a surface using numbers. It's a sort of "surface pixel" if you will. So however you want to represent your surface on the "higher level", when digitally rasterizing it, it's almost a necessity to break it down into triangles in the process. The same way it's a necessity to break any type of image into pixels if you want to display it on the screen.

                                          And GPU rasterization doesn't do anything "automatically", although it may appear so. It just delegates a lot of needed calculations to specialized parallelized hardware, instead of burdening the CPU with it. A GPU is not some magical device that pours images out onto screen. It's still just a plain old microprocessor. And like any microprocessor, it only knows how to run programs and munch data, although it's "specialized" in the sense that it prefers to munch a specific kind of data, quickly and efficiently. That quickness and efficiency is possible in great degree precisely because triangles are used for representing 3d surfaces.

                                          Infinite detail (whatever that actually means) is simply not possible using a digital computer. It's just a fantasy. Unless you stretch your definition of "infinite detail" to mean "adaptive subdivision/tessellation of analytic surfaces". That can be done (and it it done) without problems on today's hardware, but sooner or later in the process of putting it on the screen, everything needs to be broken down into triangles and then into pixels, either by the CPU or the GPU, or some other kind of *PU 🙂

                                              Megalomaniak It is trigonometry, just using less data more intelligently. Think of a normal bezier curve, even a curve drawn in the Godot menu is a good example:

                                              In this case you have 3 points you can move around in the editor, and between them you see a line. This line is smooth, not a straight line: You obtain this hump automatically just by defining the 3 points, each pixel on the line knows where it should be located based on its position in 2D space. Therefore you can only add 3 points to get a round bump, instead of needing to have say 16 points with straight lines between them to manually simulate the curve yourself and do so at a lower accuracy for more cost.

                                              My idea was what it would have been like if the GPU and OpenGL could do this in 3D space with vertices / surfaces in meshes: Instead of drawing straight triangles between vertices, treat each vertice as a curve point and draw 2D bezier curves between them. Just as for a 2D curve you know where a pixel is supposed to be between vertices by calculating the X + Y coordinates against them, in 3D you'd do the same based on X + Y + Z coordinates.

                                              Like I said I'm aware there's likely a good reason why this never happened, and whatever the reason it's likely too late now unless GPU manufacturers invent a new 3D technology (and we just got Vulkan). Godot like other engines is limited by the capabilities of the rendering technology it works with so it can't do this at hardware level even if it tried... which I guess makes me thinking about this a bit bizarre since it's pointless, didn't want this to get side-tracked from parallax but it's a concept from the same book of magic tricks that could have been used to better allow the illusion of infinite detail.

                                                xyz Infinite detail both is and isn't possible, and I think fractals like the Mandlebrot pattern illustrate it best: Each fractal is a mathematical formula, usually a very short one that only takes a few lines of code to define, yet when running it you get all those pixels on the screen. The only reason it isn't infinite is that you have a finite number of pixels in your monitor, but each pixel calculates itself at a particular position from a formula that is itself infinite and only bound by the lowest / highest number the CPU and RAM can define.

                                                As such I often wondered what it would be like if we'd have done the same with 3D. This can include a voxel based approach which is easier, there's actually a lovely software called Mandlebulber that does this with amazing results but sadly it's very slow since it's probably CPU based. But the concept could theoretically be used even with faces in conventional meshes if we interpreted them differently, such as allowing the a heightmap to change where a point on the surface is interpreted between its vertices instead of reading it as a flat triangle.

                                                    MirceaKitsune Fractals are not infinite detail. They are just potentially infinite subdivision. You can't really use fractals as a modeling tool. They are unwieldy and at the same time repetitive. They get boring very fast.

                                                    As for using non linear rendering primitives, like bezier patches for example, if you try to implement it you'll quickly see it's almost impossible to use them in such manner. There's a myriad of reasons why a linear primitive was chosen and it's not a matter of legacy. I could go into specifics but I won't until you implement a basic software rasterizer. It'll clear you mind and bring you out of the fantasy land 😉

                                                      xyz It's because of digitalization, i.e. because we're doing the thing using a digital computer.

                                                      I, too, think it's about time we moved on to quantum bio-computers and analog-vector monitors.

                                                      • xyz replied to this.

                                                          Tomcat I, too, think it's about time we moved on to quantum bio-computers and analog-vector monitors.

                                                          Why?

                                                              xyz for the semi-retro bio-punk cool factor?

                                                              MirceaKitsune But the concept could theoretically be used even with faces in conventional meshes if we interpreted them differently, such as allowing the a heightmap to change where a point on the surface is interpreted between its vertices instead of reading it as a flat triangle.

                                                              Ok, I think you are not understanding us here... We are saying that you inevitably have to decimate and rasterize to limit mesh the idealized mathematical curved surface no matter what. It's how the maths work out and the triangle is the most basic 3D element to do this with. Even CPU/Software rendered Catmull-Clark SDS still ultimately uses triangles to rasterize the limit mesh output. There's no escaping it. But as CC SDS/Reyes proved you can very successfully do 1 to 5 tris(or more even) per pixel to get a virtually infinite detail level if you have the data to render/rasterize.

                                                              Basically Catmull-Clark subdivision surfaces with vector displacement would probably be for all intents and purposes what you are after here and you're just trying to reinvent the wheel here.

                                                              edit: speaking of OpenSubdiv...
                                                              https://github.com/godotengine/godot-proposals/issues/784
                                                              https://github.com/tefusion/godot-subdiv