Yep, the distributions are uneven.
Using the method where you pick a position in a square, normalise, then scale by random distance gives you this:

This is because there is a lot of area in the corners that are outside of the circle. All that area needs to be pulled back into the circle. Or put another way, the distance from the centre to the edge is 255 pixels, but the distance from the centre to the corner is 360.
The next one is where you pick a random angle and random radius, using cos and sin (so polar coordinates).

This one bunches up in the middle.
This is because any radius has equal chance of being picked, but there's less area for pixels so they are higher density.
Here's the best one:

This is identical to the second method, pick a random angle and radius. But do a square root of the random value used for the radius. This is called inverse transform sampling.
I don't have a GDScript version, but here's the code from my C++ test that made the pics above:
kf::Vec2 p;
float angle = rnd.norm() * 3.14159265 * 2.0;
float rad = sqrt(rnd.norm()) * maxRadius;
p.x = cos(angle)*rad;
p.y = sin(angle)*rad;
rnd.norm() is my function to get a random value between 0 and 1. You must do the sqrt to the value while it's still 0 to 1.
Here's a cool page describing the technique: https://programming.guide/random-point-within-circle.html
Edit: of course most of the time nobody would notice the difference, it's only when lots of things are spawned and visible at once that the pattern is noticeable.


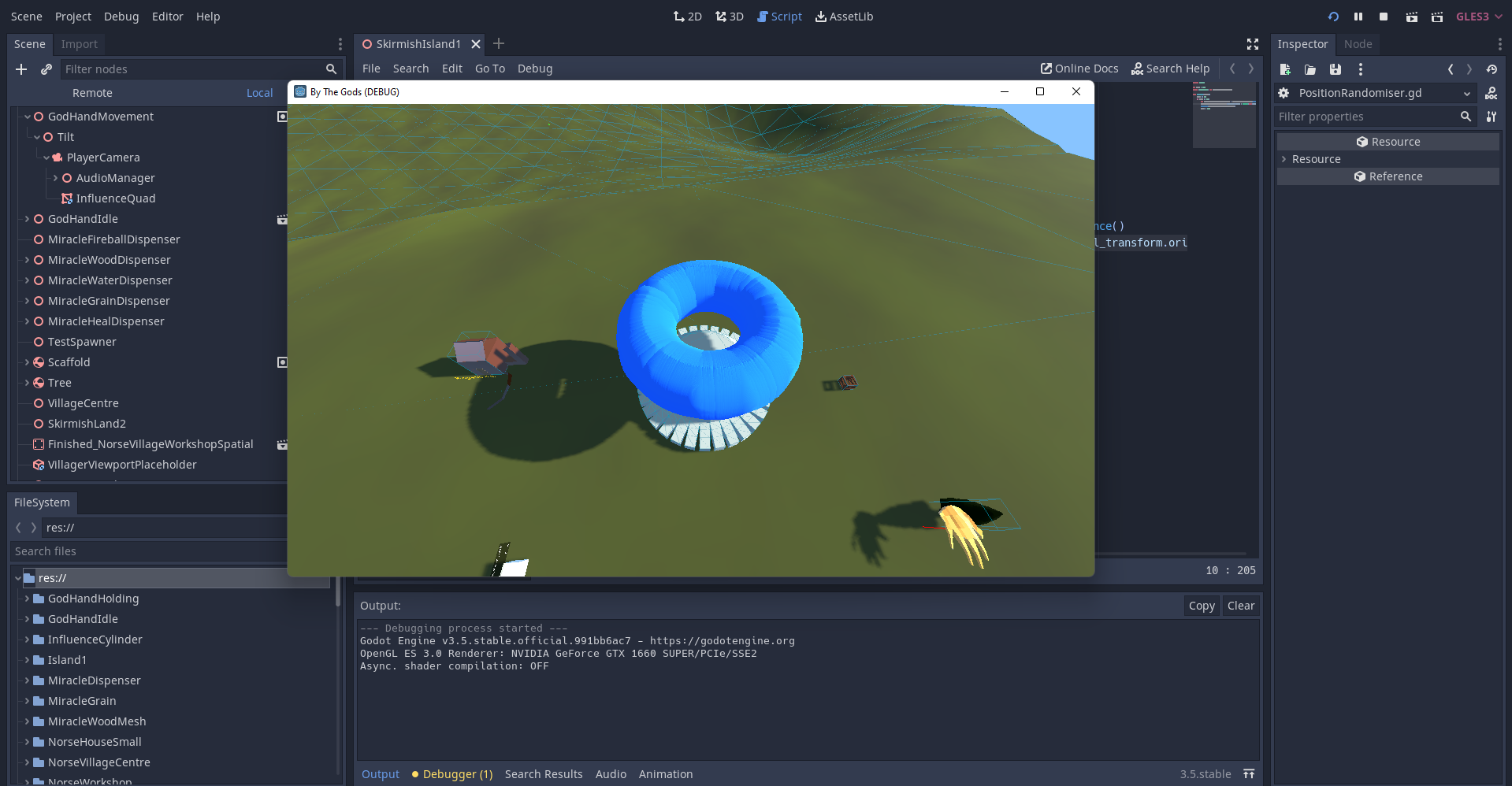
 These are actually kind of useful techniques to know because say I've got a rectangular or square room and I want the agents to wonder about in that particular area, I can do that now no problem.
These are actually kind of useful techniques to know because say I've got a rectangular or square room and I want the agents to wonder about in that particular area, I can do that now no problem.