• Godot Help

  • Setting tangents of curve points for smooth curve

how to smooth out the curve programmatically?

I have been playing with methods of the curve SetPointLeftMode and SetPointRightMode but just setting the mode is not enough:

        for (int i = 0;i < curve.PointCount; i++)
        {
            curve.SetPointLeftMode(i, Curve.TangentMode.Free);
            curve.SetPointRightMode(i, Curve.TangentMode.Free);
        }

In addition - tangent value must be set somehow with SetPointLeftTangent and SetPointRightTangent. So how do I find these values based on the "before" and "after" points' position vectors?

for example I would like to convert this curve

to

and also this

to this

programmatically.

What I tried to do is re-adding the points of the curve and setting the tangent mode to Free, hoping that the tangent values will be auto-adjusted, but this messes up the curves and they are not exactly smooth afterwards:


so any ideas how to set the tangents so the curves are smooth are appreciated..

if that matters i am using the latest godot 4 and a C# to code, but if you have some coding ideas in gdscript they are of course welcomed!

bumping 🙂 still unresolved.

I think I should clarify that I am also the one who generates the curves so I could generate as many points as possible, i.e. sine wave with 100 points.

        curve.ClearPoints();

        var resolution = 5; // number of points
        var mode = Curve.TangentMode.Linear;

        var newRes = resolution - 1;
        float sinRange = Mathf.Pi;
        float sinStep = sinRange / newRes;
        for (int i = 0; i < newRes; i++)
        {
            var x = i * sinStep;
            var y = Mathf.Sin(x);

            var normalizedX = x / sinRange;
            curve.AddPoint(new Vector2(normalizedX, y), leftMode: mode, rightMode: mode);
        }

        curve.AddPoint(new Vector2(1, 0), leftMode: mode, rightMode: mode);

        curve.Bake();

the example above will generate a sine wave with just 5 points.

regardless of the origin of the curve (hand drawn or programmatically drawn like above) - I think this question is still totally viable as I want to be able to apply the "smoothing" to the curve!

Tangent at point p can be calculated by averaging the tangents of linear segments that go from p to previous and next points.

tang_at_p = ((p-pprev).normalized() + (pnext-p).normalized()) * .5
angle_at_p = atan2(tang_at_p.y, tang_at_p.x)

    xyz hey! thank you for the formula (and help)!

    the results now look hundreds times better! Here is the code I am using in C#:

    public void SmoothCurve(Curve curve)
    {
        // Adjust the tangents to smooth the curve
        for (int i = 0; i < curve.PointCount; i++)
        {
            // Set the tangent mode to free for all points
            curve.SetPointLeftMode(i, 0);
            curve.SetPointRightMode(i, 0);

            if (i == 0)
            {
                Vector2 curPoint = curve.GetPointPosition(i);
                Vector2 nextPoint = curve.GetPointPosition(i + 1);
                /*
                float angle = Mathf.Atan2(nextPoint.Y - curPoint.Y, nextPoint.X - curPoint.X);
                float tangent = Mathf.Tan(angle);*/

                var tangentAtP = ((nextPoint - curPoint).Normalized()) * 0.5f;
                var angleAtP = Mathf.Atan2(tangentAtP.Y, tangentAtP.X);
                float tangent = angleAtP * 2;

                curve.SetPointRightTangent(i, tangent);
            }
            else if (i == curve.PointCount - 1)
            {
                Vector2 prevPoint = curve.GetPointPosition(i - 1);
                Vector2 curPoint = curve.GetPointPosition(i);

                float angle = Mathf.Atan2(curPoint.Y- prevPoint.Y, curPoint.X - prevPoint.X);
                float tangent = Mathf.Tan(angle);

                curve.SetPointLeftTangent(i, tangent);
            }
            else
            {
                // Compute the tangents for the current point
                Vector2 prevPoint = curve.GetPointPosition(i - 1);
                Vector2 curPoint = curve.GetPointPosition(i);
                Vector2 nextPoint = curve.GetPointPosition(i + 1);

                var tangentAtP = ((curPoint - prevPoint).Normalized() + (nextPoint - curPoint).Normalized()) * 0.5f;
                var angleAtP = Mathf.Atan2(tangentAtP.Y, tangentAtP.X);
                float inTangent = angleAtP * 2;
                float outTangent = angleAtP * 2;
                
                /*
                // also works
                float angle = Mathf.Atan2(curPoint.Y- prevPoint.Y + nextPoint.Y - curPoint.Y, curPoint.X - prevPoint.X + nextPoint.X - curPoint.X);
                float tangent = Mathf.Tan(angle);
                float inTangent = tangent;
                float outTangent = tangent;*/

                // Set the tangents for the current point
                curve.SetPointLeftTangent(i, inTangent);
                curve.SetPointRightTangent(i, outTangent);
            }
        }
    }

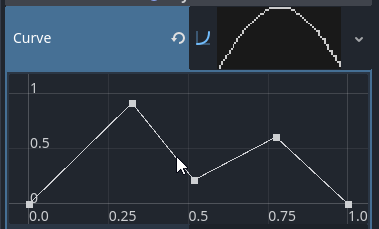
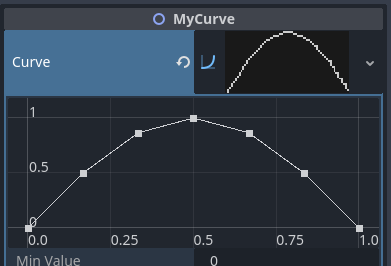
    Before:

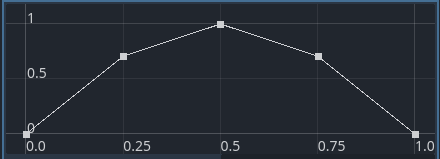
    After:

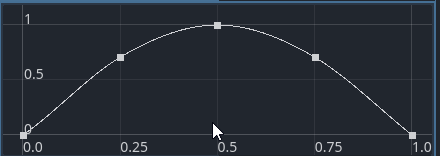
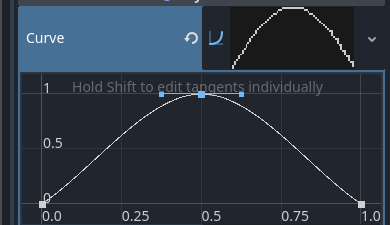
    If there is one thing to complain about, is, I believe that starting and ending points are not having the correct tangents. If you check the curve:

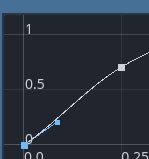
    See that the angle for the first point a bit under the curve. Per my understanding a correct angle would look like this:

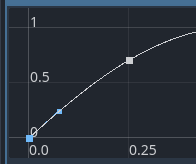
    either touching or slightly above the curve.. Is there something I am missing still or is the result works as expected?

    I tried alternative solution that I came up with

    float angle = Mathf.Atan2(nextPoint.Y - curPoint.Y, nextPoint.X - curPoint.X);
float tangent = Mathf.Tan(angle);

    but it does not work as intended either..

      If we presuppose that curvature at point 0 should be the same as curvature at point 1, then calculate the angle needed to go from vector p1-p0 to tangent at p1. Subtract this angle from already known angle of the vector p1-p0. This should give you the tangent angle at p0. You might need to clamp it to valid range, depending on how "sharp" the angle between segments at p1 is.
      Same for the last point, just in reverse.