How does the cubic_interpolate(a, b, c, d, e) operator work? I haven't been able to find any documentation on it. (Sorry if I'm using the term "operator" incorrectly here, I don't know what else to call it)
Cubic interpolation operator?
- Edited
I've not used it, but based on this in the docs:

I assume this function essentially returns a point on a cubic bezier curve between two Vectors, where pre_a/b are the handles and the weight is effectively % progress along the curve.
To understand cubic bezier curves more I'd suggest this clip, noting the 4 white circles are Vectors a/b and handles pre_a/b:
As a use case example (noting there are probably better ways to do this), I imagine you could use this function to calculate a symmetrical arc (such as for an arrow firing) between two points, say Vector2(0,0) to Vector2(0,5), by assigning Pre_a and Pre-b to directly 'above' these points Vector2(2,0) and Vector2(2,5).
- Edited
I don't do 2D, but I've roughed up a quick example of what I described above, where I'm just setting the pre_a and pre_b handles to be 'arcHeight' above their respective Origin/Target vectors.:
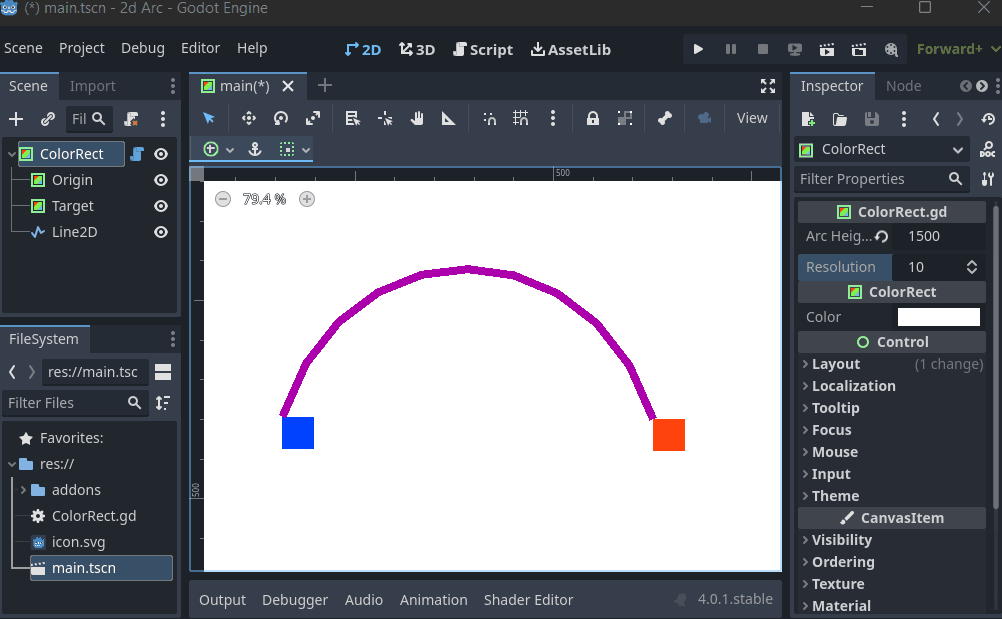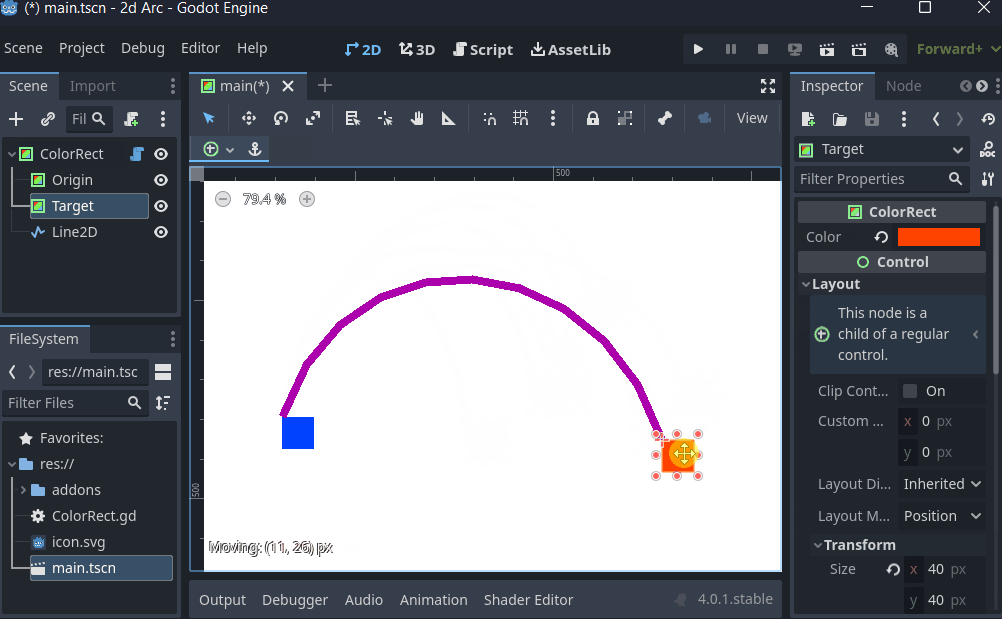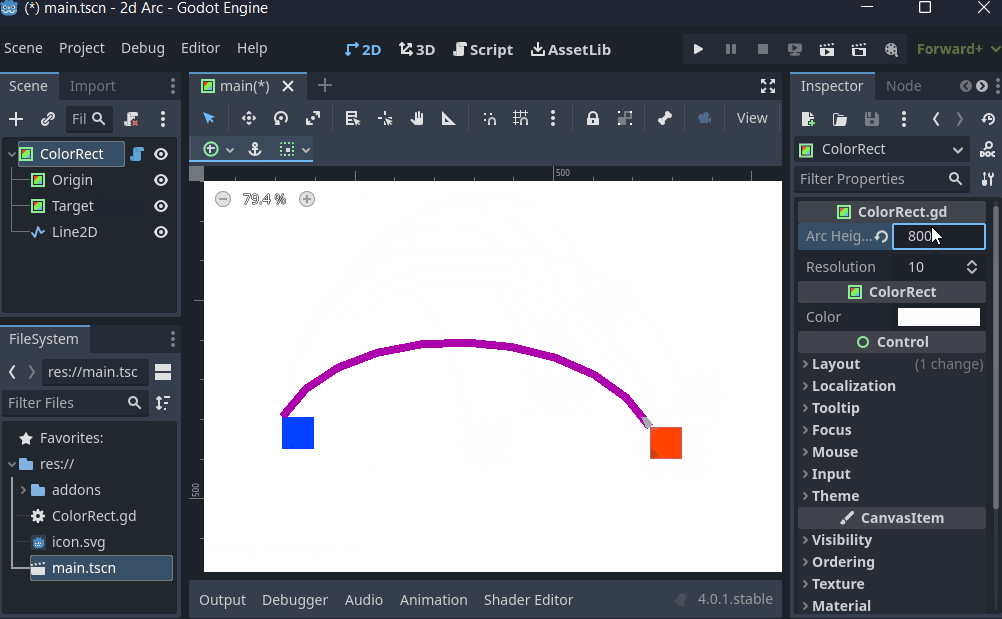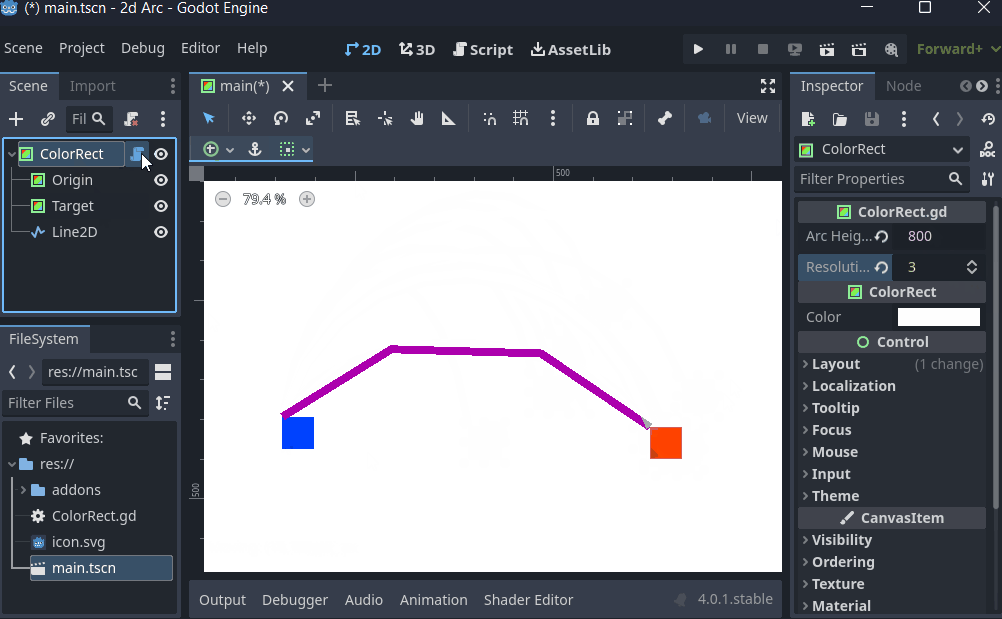
@tool
extends ColorRect
@export var arcHeight := 50.0
@export var resolution := 10
# Called when the node enters the scene tree for the first time.
func _ready():
pass # Replace with function body.
# Called every frame. 'delta' is the elapsed time since the previous frame.
func _process(delta):
var curvepoints = PackedVector2Array()
for idx in range(0,resolution+1):
curvepoints.append($Origin.position.cubic_interpolate($Target.position, Vector2($Origin.position.x,$Origin.position.y+arcHeight), Vector2($Target.position.x,$Target.position.y+arcHeight), float(idx)/float(resolution)))
$Line2D.points = curvepointsYou could then alter the profile of the curve by offseting the pre_a/b vectors as desired, or programmatically alter arcHeight depending on other factors.
Again I don't do 2D, but I imagine you could also use this to sample points along this trajectory to identify collisions for example and stop the curve early. Someone feel free to chip on what the 'best' way to do this would be.
Edit: More fun stuff, by editing the positions of pre_a and pre_b relative to origin/target vectors you can get easy bendy splines (though would need to tweak to your liking:
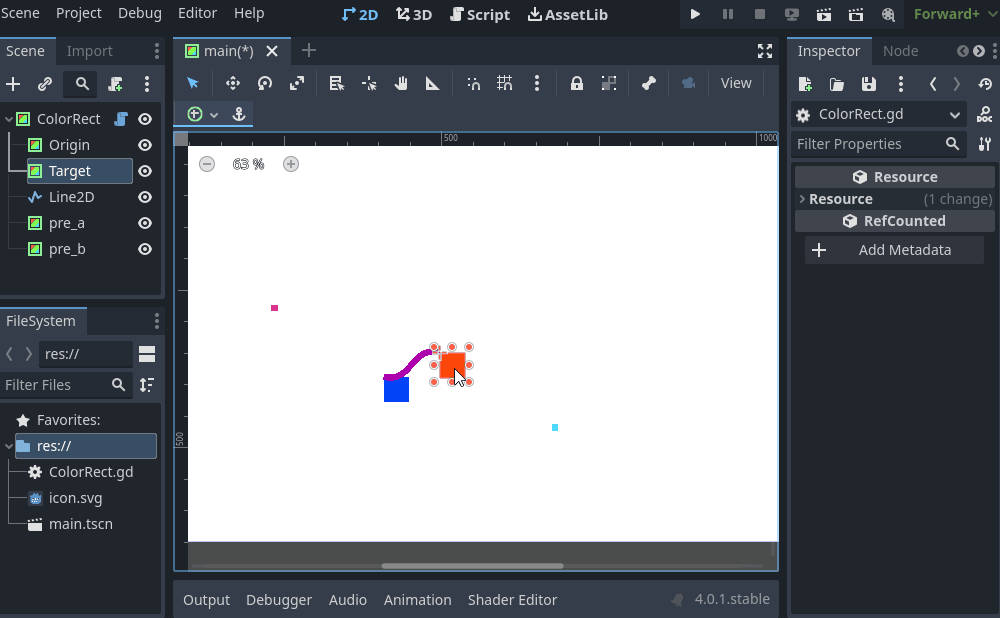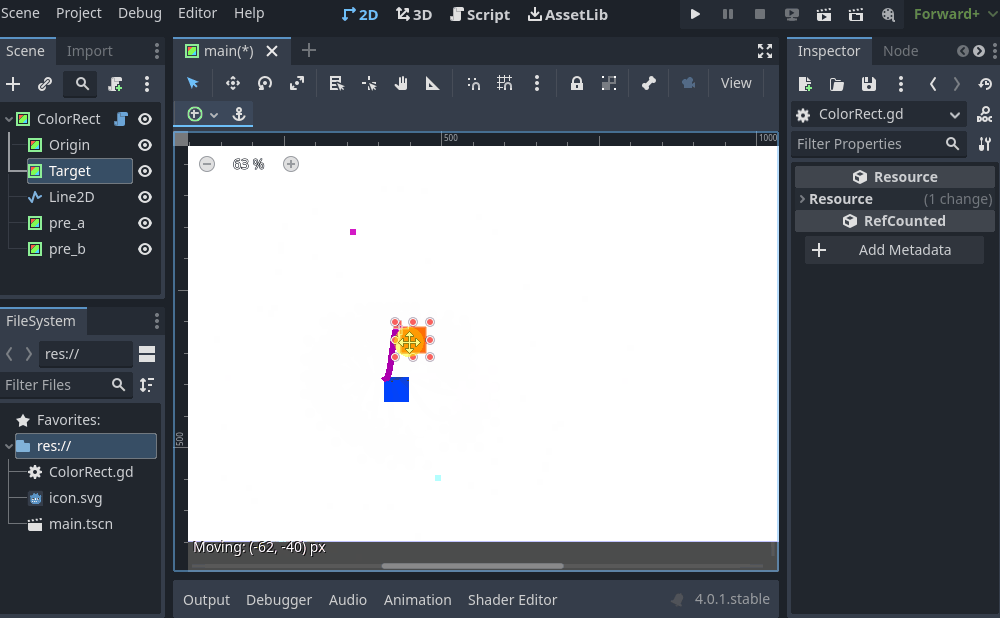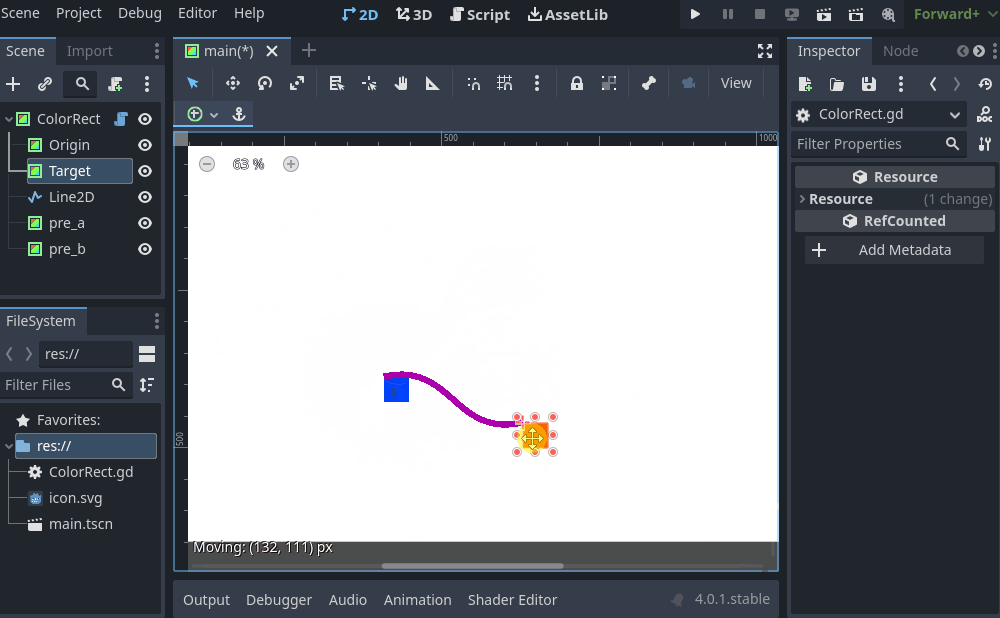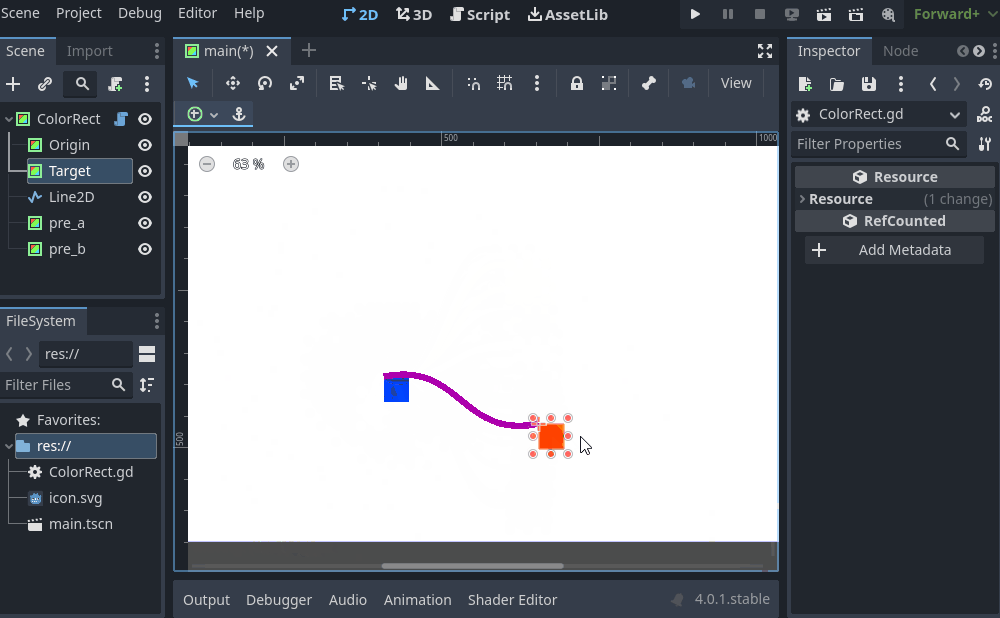
and the code:
@tool
extends ColorRect
@export var resolution := 10
# Called when the node enters the scene tree for the first time.
func _ready():
pass # Replace with function body.
# Called every frame. 'delta' is the elapsed time since the previous frame.
func _process(delta):
var curvepoints = PackedVector2Array()
$pre_a.position = Vector2($Origin.position.x+($Target.position.x - $Origin.position.x)*0.3,$Target.position.y+($Target.position.y-$Origin.position.y)*2.0)
$pre_b.position = Vector2($Target.position.x+($Origin.position.x - $Target.position.x)*0.3,$Origin.position.y+($Origin.position.y-$Target.position.y)*2.0)
for idx in range(0,resolution+1):
curvepoints.append($Origin.position.cubic_interpolate($Target.position, $pre_a.position, $pre_b.position, float(idx)/float(resolution)))
$Line2D.points = curvepointsWhen might you use something like this (at least in3D)?

- Edited
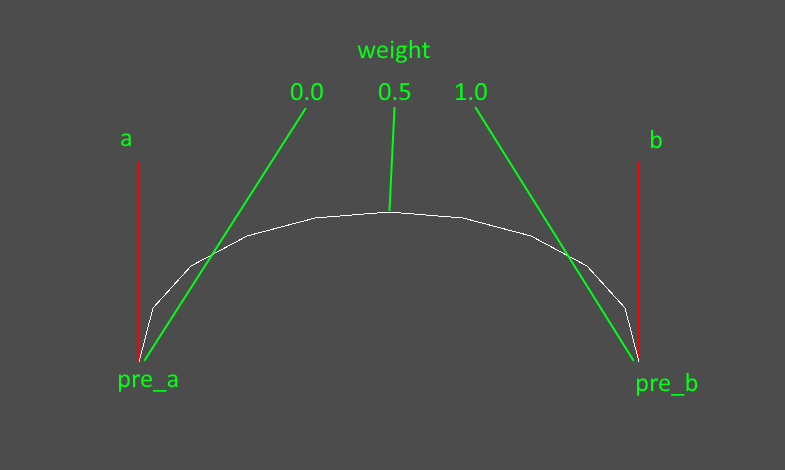
Drawn using Godot (not the green bits, that was Paint.net):

Given vectors a, b, pre_a and pre_b, the function a.cubic_interpolate(b,pre_a,pre_b,weight) will generate points along the white curve between a and b, based on the weight (0 gives a, 1 gives b, other values are between them).
So a and b are the start and end of the curve, while pre_a and pre_b are control points that influence the shape of the curve.
There's also bezier_interpolate which is a different kind of curve. Using the same variables, this:
pre_a.bezier_interpolate(a, b, pre_b, weight
would generate this curve:
Edit: oops, beaten to it by Bimbam.
